
在量子理论中,复数长期以来被视为不可或缺的数学工具,但近年来研究表明,实数足以模拟复数的所有关键性质。实数量子理论(Real-Number Quantum Theory, RNQT),它通过巧妙的映射和组合规则,用实数矩阵完全复现了复数量子理论(QT)的统计预测和行为。以下我将逐步解释如何用实数模拟虚数,重点关注核心映射、组合规则和关键性质如表示局部性。回复结构将包括背景动机、具体映射方法、多系统处理、理论一致性以及总结。
1. 背景动机:为什么需要实数模拟?
量子理论传统上基于复数希尔伯特空间,但历史上一直存在争论:复数是否是本质的,还是仅是一种便利。早期尝试(如Stückelberg的工作)用实数表示量子理论,但未能满足表示局部性(representation locality),即物理上局部的操作应在数学表示上也是局部的。RNQT指出,关键在于张量积的矩阵表示:复数QT中常用Kronecker积,但实数理论中需定义新组合规则(如⊗ᵣ),才能保持一致性。
2. 核心映射:Γ映射——将复数矩阵转换为实数矩阵
实数模拟复数的核心是一种称为Γ的映射,它将复数矩阵注入到实数矩阵空间中,同时保持内积、正定性和代数结构。具体步骤如下:

3. 多系统处理:组合规则⊗ᵣ——保持张量积结构
在量子理论中,多系统组合通过张量积(postulate iv)描述。实数理论需定义一种新组合规则⊗ᵣ(而非Kronecker积⊗_K),以确保表示局部性和统计一致性:
⊗ᵣ规则的定义:对于两个特殊对称矩阵S和T(即Γ映射的图像),其组合规则为:
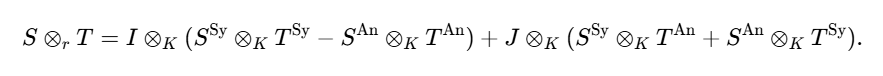
这模仿了复数张量积的行为,例如 (a+ib)(c+id)的实部与虚部组合。
关键性质:⊗ᵣ规则是关联的、保持内积,并满足
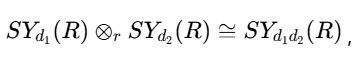
这意味着多系统状态能正确嵌入实数空间,且局部操作仅影响局部数学表示(即表示局部性)。
4. 表示局部性:实数理论的关键优势
表示局部性是实数理论成功模拟复数的关键。它确保物理上局部的操作(如仅对第一个原子施加激光)在数学表示上也是局部的,即状态更新形式为 ρ′⊗σ而非全局操作 h′(ρ⊗σ)。文档用以下图片直观说明这一概念:
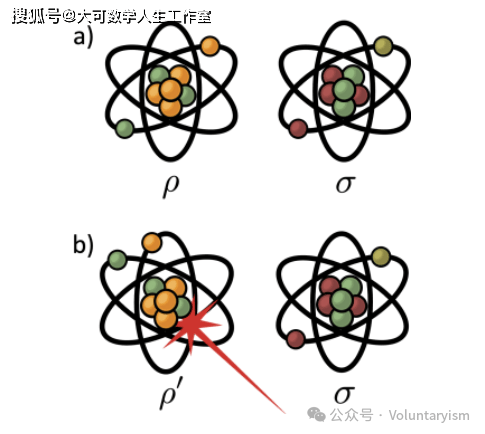
如图1所示,在表示局部的理论中,两个独立制备的原子状态表示为 ρ⊗σ,当仅第一个原子受激光影响时,数学更新为 ρ′ ⊗σ(局部更新)。若非局部表示,则需全局操作 h′ (ρ⊗σ),这会破坏物理直觉。实数理论通过⊗ᵣ规则实现了这一点,而早期尝试(使用Kronecker积)失败于此。
5. 理论一致性:RNQT如何复现QT的统计
RNQT通过以下方式确保与QT实验不可区分:
状态与测量的映射:定义映射M(用于状态)和E(用于测量),例如

将QT对象线性映射到RNQT的特殊对称矩阵集合。
Born规则保持:概率计算满足
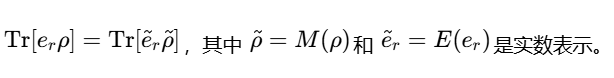
动态扩展:RNQT还包含实数版本的冯·诺依曼方程,描述封闭系统演化,其中哈密顿量等也通过Γ映射转换为实数形式。
6. 总结与展望
实数模拟虚数的核心在于Γ映射和⊗ᵣ组合规则,它们将复数的代数结构编码到实数矩阵中,同时保持表示局部性等关键性质。RNQT不仅解决了Schrödinger等历史争议,还表明复数在量子理论中的角色类似于经典波理论中的复数——一种数学便利而非本质需求。这为统一广义相对论和量子理论提供了新视角。
总之,实数通过结构化映射(如Γ)和自定义组合规则(如⊗ᵣ)能完全模拟虚数,确保了量子理论的预测能力和物理直觉。文档中的严格证明和示例(如贝尔态的处理)进一步验证了这一点。
二、量子力学:工具性与本体性的激烈争论
在量子力学中,复数i 的地位存在深刻分歧:
工具性观点:部分物理学家认为,复数是描述量子态的便捷语言,但并非本质必需。例如:
2008 年和 2009 年的研究表明,通过将希尔伯特空间维度加倍(即用两个实数替代一个复数),可构建与标准量子理论等价的实数形式。
2025 年,德国与法国团队提出新的实数理论,通过修改张量积规则,成功重现了复数理论的所有实验预测。
谷歌量子 AI 团队的研究表明,量子算法中的 T 门(涉及复数旋转)可被实数操作替代,尽管会增加计算步骤。
本体性观点:复数是量子力学的内在结构,具有不可替代性:
薛定谔方程的幺正性:方程中的 i 确保概率守恒(∫∣Ψ∣²dr=1),若移除 i,方程将退化为热传导方程,破坏量子态的可逆性。
量子纠缠的不可分离性:2021 年西班牙、奥地利等国的实验(纠缠交换实验)以 43 个标准差排除了实数理论,证明复数相位是描述量子纠缠的必要条件。
量子干涉的本质:双缝实验中,复数波函数的相位差 Δϕ 直接决定干涉条纹的位置,实数理论无法自然生成干涉项。
当前态势:尽管存在实数重构的尝试,但复数理论在数学简洁性、物理直观性和实验验证上仍占据主导地位。中国科学技术大学潘建伟团队的实验(43 个标准差)和南方科技大学范靖云团队的实验均支持复数的必要性。
三、数学基础与哲学层面的深层分歧
代数闭包性:复数域 C 是实数域 R 的唯一代数闭包,任何多项式方程在C中必有解。这种数学完备性使复数在描述物理规律时具有天然优势。
解析函数的刚性:复分析中的全纯函数具有 “局部决定全局” 的特性(如柯西积分公式),这与物理中的守恒律(如能量守恒)高度契合。
实在论与工具论的对立:
实在论者认为,复数的普遍性暗示宇宙可能具有复结构,i 是自然规律的基本语言。
工具论者坚持,复数仅是人类发明的高效符号系统,与物理实在无关。
四、总结:共识的边界与动态演变
工程与经典物理:复数是高效工具的共识,非物理必需。
量子力学:复数是实用框架的共识,但本体性争议仍存。主流观点认为其不可替代,但实数重构的理论探索持续进行。
数学与哲学:复数的代数完备性和解析刚性被广泛认可,但其物理实在性尚未达成一致。
最终结论:在工程和经典物理中,复数 i 的工具性共识明确;在量子力学中,复数是描述微观世界的标准语言,但严格的 “必要性” 仍存在理论争议。“复数在工程中是高效工具必需,在量子力学中是物理本质必需”。
它触及了量子力学基础的一个核心问题:复数在量子理论中是否是必不可少的?
我们可以分几个层面来理解:
1. 标准量子理论:复数是核心
在我们熟悉的标准量子力学中,复数 扮演着至关重要的角色:
波函数: 系统的状态由一个复数波函数ψ描述。
薛定谔方程: 时间演化的核心是虚数单位 i:iℏ ∂ψ/∂t = Ĥ ψ。
对易关系: 位置和动量算符之间著名的对易关系 [x̂, p̂] = iℏ 也包含了 i。
相位干涉: 量子叠加和干涉现象(如双缝实验)本质上是复数的相位在起作用。
长期以来,物理学家和数学家都认为复数是量子理论不可或缺的、最自然的数学语言。
2. 实数版量子理论:
具体来说,构建一个“实数量子力学”通常意味着:
实数的希尔伯特空间: 将状态向量定义为实矢量空间中的元素,而不是复矢量空间。
实数的算符: 所有物理可观测量(如哈密顿量)都由实对称算符表示,而不是厄米算符(厄米算符要求对角元素为实,非对角元素为共轭对称)。
修改对易关系: 例如,将 [x̂, p̂] = iℏ 替换为另一种形式,比如引入两个实数的算符来实现类似的效果。
3. 关键问题:两者是否等价?
这引出了核心的科学问题:标准的复数量子力学和这个假设的实数量子力学,在物理预言上是否可以区分?
历史上,人们普遍认为它们是等价的,可以通过一个简单的“重新包装”将复数理论转化为实数理论。
一个简单的对应关系:
任何一个复数的波函数 ψ 都可以分解为实部和虚部:
ψ = ψ_re + i ψ_im
那么,这个单一的复数量子态,就可以用一个二维的实列向量来表示:
Ψ_real = [ψ_re, ψ_im]^T
这样一来,复希尔伯特空间中的态,就对应于一个维数加倍的实希尔伯特空间中的态。复数的相位信息被编码在了这两个实分量的相对关系中。
4. 近年来的重大突破:它们可以被区分!
尽管上述数学对应关系存在,但近年来的理论研究(特别是来自中国科大潘建伟院士团队的研究)表明,在更复杂的场景下,复数在量子力学中不仅仅是数学上的便利,它会产生可观测的物理效应。
2026年的理论工作(2022年发表):
潘建伟团队的理论学家提出了一种具体的方案,可以设计一个实验来检验量子理论是否需要复数。
核心思想: 他们构造了一个基于实数版本的“局域隐变量理论”和标准复数量子理论的贝尔不等式变体。
实验设计: 设计一个特定的量子纠缠态和一组特定的测量方式。在这个精心设计的设置下:
如果量子力学是实数的,那么测量结果的关联会有一个上限。
如果量子力学是复数的,那么测量结果的关联会突破这个上限。
结论: 这就提供了一个清晰的、可检验的判据来区分“实数量子论”和“复数量子论”。
2022年的实验验证:
同一个团队随后在实验上实现了这个构想。他们利用光学系统制备了所需的纠缠态并进行了精确测量。实验结果明确地违反了实数理论所设定的上限,而与复数量子理论的预言完美符合。
这个实验被广泛认为是首次在定域性和实数性这两个“经典”假设上,同时验证了量子力学的非经典性,证明了复数是量子力学中不可或缺的“自然资源”。
总结
所以,“实数版量子理论”可以理解为:
一个理论框架: 一种尝试只用实数构建的、在数学上自洽的量子理论。
一个检验工具: 它作为一个“假想敌”,帮助我们通过对比来更深刻地理解标准复数量子理论的本质特征。
一个已被证伪的假设: 最新的理论和实验表明,虽然可以数学地构造出实数版量子理论,但我们的物理世界选择了那个需要复数描述的、更丰富的版本。复数不是数学上的冗余,而是物理现实的内在属性。
简单来说,实数版量子理论就像是一个“黑白电视”的模型,而我们的世界是一台“彩色电视”。 虽然黑白模型也能描述很多现象,但只有彩色模型才能完整、准确地反映所有细节。实验证明,我们的宇宙是“彩色”的。
)
)
)
)
)
)

)
)

)
)

)

)